This document provides a comprehensive walk-through of the meta-analysis investigating the efficacy of psilocybin for treating depression symptoms, using data extracted for the SYPRES project. The analysis includes both continuous (depression symptom severity scores) and dichotomous (response/remission rates) outcomes, along with extensive subgroup and sensitivity analyses.

Our database for this analysis can be accessed through the R package metapsyData. It can also be downloaded directly as a CSV file here. Documentation on metapsyData is available here.

The meta-analytic portion of this script primarily uses the R package metapsyTools. Documentation on metapsyTools is available here.

This walk-through has some code chunks hidden for clarity. Full source code for this analysis is available here.

Overview

This meta-analysis synthesizes evidence from randomized controlled trials examining the efficacy of psilocybin for treating depression. The analysis employs meta-analytic methods to provide robust estimates of treatment effects while accounting for study heterogeneity and potential biases.

Key Features of This Analysis

  • Comprehensive outcome assessment: Both continuous (depression symptom severity) and dichotomous (response/remission) outcomes
  • Time course analysis: Three-level hierarchical models to examine treatment effects over time
  • Robustness testing: Extensive sensitivity and subgroup analyses
  • Publication bias assessment: Multiple methods to evaluate potential bias
  • Transparent reporting: Complete code and methodology documentation

Methods

Key statistical specifications:

  • Effect size: Hedges’ g for continuous outcomes, log RR for dichotomous outcomes
  • Heterogeneity estimator: REML for random-effects models
  • Confidence intervals: Q-Profile method for heterogeneity, Knapp-Hartung adjustment for effect sizes
  • Significance testing: Knapp-Hartung adjustment for small sample sizes

Quality Assessment

We conduct sensitivity analyses excluding studies with high risk of bias evaluated using the Cochrane Risk of Bias tool. Publication bias is evaluated using a funnel plot and Egger’s test.

Load Required Packages

We begin by loading the necessary R packages for data manipulation, meta-analysis, and visualization:

  • Data manipulation: readr and tidyverse for data loading and manipulation
  • Meta-analysis: meta and metafor for conducting meta-analytic calculations
  • Effect sizes: esc for effect size calculation utilities
  • Specialized tools: metapsyTools for specific meta-analysis functions and dmetar for additional meta-analysis tools
library(readr)
library(tidyverse)
library(meta)
library(metafor)
library(metapsyTools)
library(metapsyData)
library(gt)
library(dmetar)
library(bayesmeta)

Data Loading and Quality Checks

The sypres database depression-psiloctr is downloaded using the metapsyData package. Before proceeding with the analysis, we perform quality checks to ensure data integrity and identify potential issues.

# Load data using metapsyData
d <- getData("depression-psiloctr")
data <- d$data


# Check data format with checkDataFormat
checkDataFormat(data)

# Check conflicts with checkConflicts
checkConflicts(data,
  vars.for.id = c(
    "study", "outcome_type",
    "instrument", "study_time_point",
    "time_weeks",
    "rating"
  )
)

Data Preparation and Filtering

We prepare the data for analysis by applying several filters to create our primary analysis dataset:

  1. Primary outcomes: Select only the primary instrument and timepoint for each study
  2. Study design: Exclude post-crossover data to avoid double-counting
  3. Outcome type: Include only endpoint data (mean/SD or imputed mean/SD)
  4. Dosing: Exclude medium-dose arm (10 mg psilocybin) from multi-arm study (Goodwin 2022)
  5. Study exclusions: Remove specific studies (Grob 2011, Krempien 2023, Carhart-Harris 2021) based on predefined criteria

The resulting data_main dataframe contains the filtered data ready for our primary meta-analysis.

data_main <- data %>%
  filterPoolingData(
    primary_instrument == "1",
    primary_timepoint == "1",
    is.na(post_crossover) | !Detect(post_crossover, "1"),
    outcome_type == "msd" | outcome_type == "imsd",
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm1)) & Detect(multi_arm1, "10 mg")),
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm2)) & Detect(multi_arm2, "10 mg")),
    !Detect(study, "Krempien 2023"),
    !Detect(study, "Carhart-Harris 2021")
  )

Results

Primary Meta-Analysis

We conduct the main meta-analysis using the runMetaAnalysis function from metapsyTools. This analysis pools all studies in our filtered dataset to estimate the overall effect of psilocybin on depression severity.

Key specifications:

  • Effect size: Hedges’ g (standardized mean difference)

  • Model: Random-effects meta-analysis using REML estimator

  • Adjustments: Knapp-Hartung adjustment for significance tests

  • Additional analyses: Outlier detection and removal

The results include the pooled effect size, confidence intervals, heterogeneity statistics, and the meta-analysis model object.

main_results <- runMetaAnalysis(data_main,

  # Specify models to run
  which.run = c("overall", "outliers"),
  which.influence = "overall",
  which.outliers = "overall",

  # Specify statistical parameters
  es.measure = "g", # Hedges' g
  method.tau = "REML",
  method.tau.ci = "Q-Profile",
  hakn = TRUE, # Knapp-Hartung adjustment

  # Specify variables
  study.var = "study",
  arm.var.1 = "condition_arm1",
  arm.var.2 = "condition_arm2",
  measure.var = "instrument",
  w1.var = "n_arm1",
  w2.var = "n_arm2",
  time.var = "time_weeks",
  round.digits = 2
)

summary(main_results$model.overall)

##                      g             95%-CI %W(random)
## Back 2024      -1.4215 [-2.2271; -0.6160]        6.9
## Davis 2021     -2.4807 [-3.5637; -1.3976]        4.7
## Goodwin 2022   -0.7092 [-1.0308; -0.3876]       13.7
## Griffiths 2016 -1.2731 [-1.8827; -0.6635]        9.2
## Lewis 2025     -1.7297 [-2.7230; -0.7365]        5.3
## Luquiens 2025  -0.3347 [-1.0987;  0.4294]        7.3
## Raison 2023    -0.8700 [-1.2941; -0.4459]       12.0
## Rieser 2025    -0.3806 [-1.0314;  0.2701]        8.7
## Rosenblat 2024 -0.1417 [-0.8599;  0.5765]        7.8
## Ross 2016      -0.7940 [-1.5967;  0.0086]        6.9
## Ross 2025      -0.8275 [-1.5562; -0.0988]        7.7
## von Rotz 2023  -0.9384 [-1.5120; -0.3648]        9.7
## 
## Number of studies: k = 12
## 
##                                 g             95%-CI     t p-value
## Random effects model (HK) -0.9031 [-1.2561; -0.5501] -5.63  0.0002
## Prediction interval               [-1.7283; -0.0778]              
## 
## Quantifying heterogeneity:
##  tau^2 = 0.1174 [0.0140; 1.0125]; tau = 0.3427 [0.1185; 1.0062]
##  I^2 = 53.9% [11.4%; 76.0%]; H = 1.47 [1.06; 2.04]
## 
## Test of heterogeneity:
##      Q d.f. p-value
##  23.84   11  0.0134
## 
## Details on meta-analytical method:
## - Inverse variance method
## - Restricted maximum-likelihood estimator for tau^2
## - Q-Profile method for confidence interval of tau^2 and tau
## - Hartung-Knapp adjustment for random effects model (df = 11)
## - Prediction interval based on t-distribution (df = 10)

# Create simple forest plot of results

meta::forest(
  main_results$model.overall,
  sortvar = main_results$model.overall$data$year,
  layout = "JAMA"
)

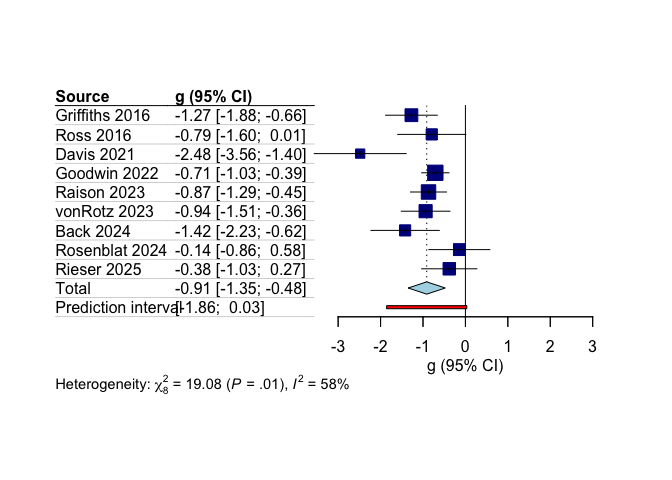
The primary meta-analysis on continuous outcomes in the 12 studies included in the main model showed a statistically significant reduction in depression scores with psilocybin treatment as compared to control conditions, with small to moderate between-study heterogeneity.

Publication Bias Assessment

We assess potential publication bias using both visual (funnel plot) and statistical (Egger’s test) methods.

# Run Egger's test

eggers.test(main_results$model.overall)

## Eggers' test of the intercept 
## ============================= 
## 
##  intercept       95% CI      t         p
##     -1.575 -3.88 - 0.73 -1.338 0.2105826
## 
## Eggers' test does not indicate the presence of funnel plot asymmetry.

png(filename = file.path(basedir, "analysis/psilodep/paperfigs/SI_Fig_01.png"), res = 315, width = 2500, height = 1500)
funnel(main_results$model.overall,
  studlab = TRUE, # can also use vector with study labels
  cex.studlab = 0.7, # adjust size of study labels
  cex = 0.7, # axis tick labels and point size
  cex.axis = 0.7, # axis number label size
  cex.lab = 0.7, # axis title (xlab, ylab) size
  cex.main = 0.95, # main title size
  xlim = c(-3, 0.2),
  col = "steelblue",
  pch = 19, # bold solid circle
  bg = "white",
  xlab = "Standardized Mean Difference (SMD)",
  ylab = "Standard Error (SE)",
  main = "Funnel Plot of Main Model Continuous Outcomes",
  las = 1
)
dev.off()

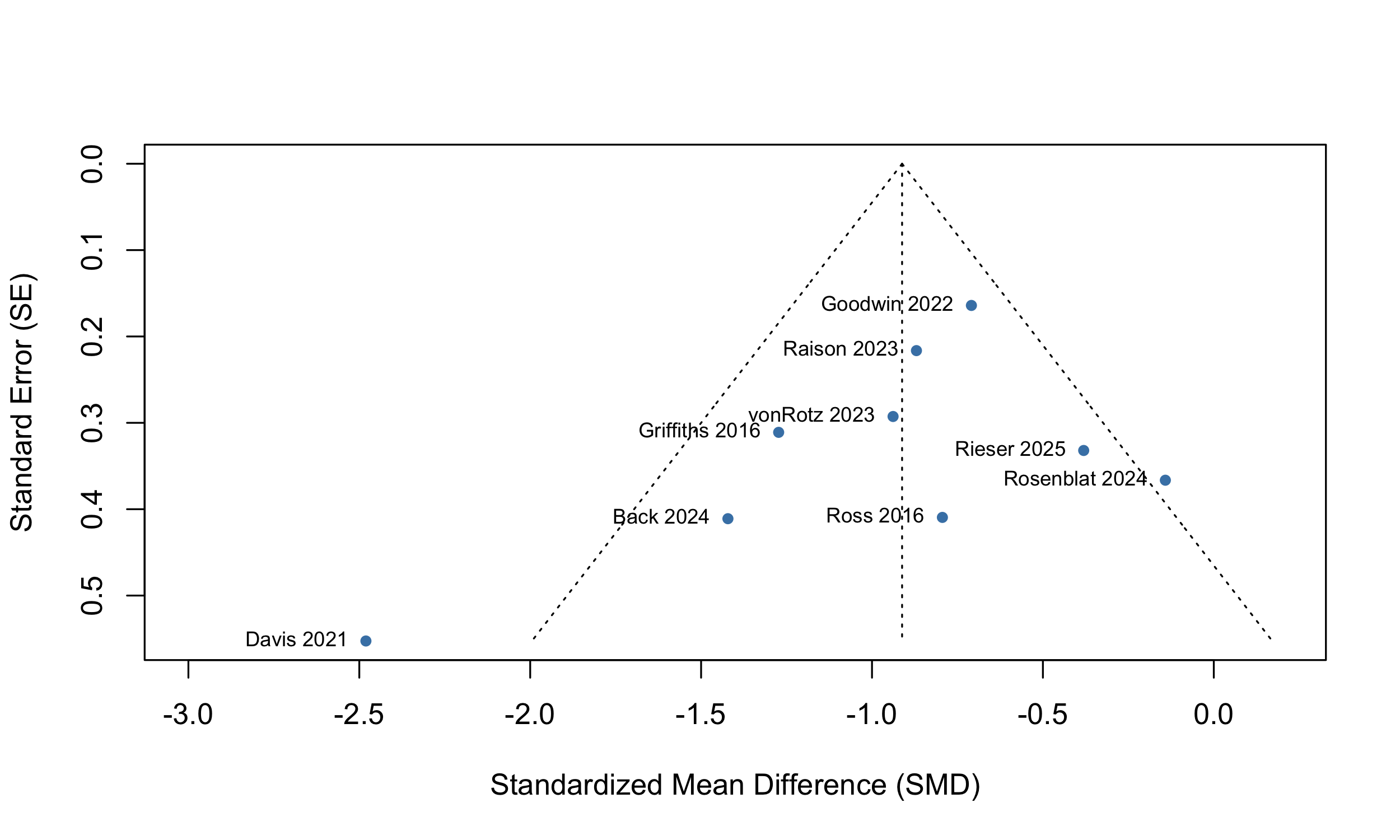Visual inspection of the funnel plot reveals limited asymmetry, and the Egger’s test did not find small study effects, implying minimal evidence of publication bias.

Three-level correlated and hierarchical effects (CHE) meta-analysis

We conduct a three-level correlated and hierarchical effects (CHE) meta-analysis to examine how the effect of psilocybin changes over time. This approach accounts for the hierarchical structure of the data (multiple timepoints within studies) and potential correlations between timepoints.

# Select data for the CHE meta-analysis

data_time <- data %>%
  filter(
    is.na(multi_arm1) | !str_detect(multi_arm1, "10 mg"),
    is.na(multi_arm2) | !str_detect(multi_arm2, "10 mg"),
    !str_detect(study, "Krempien 2023"),
    !str_detect(study, "Carhart-Harris 2021")
  ) %>%
  filterPoolingData(
    primary_instrument == "1",
    time_days > 0,
    post_crossover == 0 | is.na(post_crossover),
    outcome_type == "msd" | outcome_type == "imsd"
  )

# Run meta-analysis

time_results <- runMetaAnalysis(data_time,
  which.run = "threelevel.che",
  # Specify statistical parameters
  es.measure = "g", # Hedges' g
  method.tau = "REML",
  method.tau.ci = "Q-Profile", # N/A for three-level models
  # i2.ci.boot = TRUE, # Need to use bootstrapping to get het. CI on three-level
  hakn = TRUE, # Knapp-Hartung adjustment

  # Specify variables
  study.var = "study",
  arm.var.1 = "condition_arm1",
  arm.var.2 = "condition_arm2",
  measure.var = "instrument",
  w1.var = "n_arm1",
  w2.var = "n_arm2",
  time.var = "time_days",
  round.digits = 2
)

time_results$model.threelevel.che

## 
## Multivariate Meta-Analysis Model (k = 37; method: REML)
## 
## Variance Components:
## 
##             estim    sqrt  nlvls  fixed       factor 
## sigma^2.1  0.0822  0.2866     12     no        study 
## sigma^2.2  0.0450  0.2121     37     no  study/es.id 
## 
## Test for Heterogeneity:
## Q(df = 36) = 94.2903, p-val < .0001
## 
## Model Results:
## 
## estimate      se     tval  df    pval    ci.lb    ci.ub      
##  -0.8221  0.1254  -6.5542  36  <.0001  -1.0765  -0.5677  *** 
## 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The three-level CHE model reveals an overall significant decrease in depression scores under psilocybin compared to control conditions.

The CHE model assumes that there is a known correlation “rho” between effect sizes in the same study; and that “rho” has the same value within and across all studies in our meta-analysis (the “constant sampling correlation” assumption, J. E. Pustejovsky and Tipton 2021). While these authors have reported that “meta-regression coefficient estimates were largely insensitive to assuming different values of rho between 0.0 and 0.8”, our default choice of rho = 0.6 in metapsyTools is nonetheless, a guess. It is therefore generally recommended to run sensitivity analyses for varying values of rho:

# sweep rho in the CHE model for r = seq(0, 1, 0.1)
rho_seq <- seq(0, 1, 0.1)
i <- 1
g_sweep <- numeric(length(rho_seq))
g_ci_lwr <- numeric(length(rho_seq)) # Initialize the vector
g_ci_upr <- numeric(length(rho_seq)) # Initialize the vector

for (rho in rho_seq) {
  time_results_sweep <- runMetaAnalysis(data_time,
    which.run = "threelevel.che",
    # Specify statistical parameters
    es.measure = "g", # Hedges' g
    method.tau = "REML",
    method.tau.ci = "Q-Profile", # N/A for three-level models
    hakn = TRUE, # Knapp-Hartung adjustment
    rho.within.study = rho,
    # Specify variables
    study.var = "study",
    arm.var.1 = "condition_arm1",
    arm.var.2 = "condition_arm2",
    measure.var = "instrument",
    w1.var = "n_arm1",
    w2.var = "n_arm2",
    time.var = "time_days",
    round.digits = 2
  )

  g_sweep[i] <- time_results_sweep$summary$g[2]
  g_ci <- as.numeric(
    strsplit(gsub("\\[|\\]", "", time_results_sweep$summary$g.ci[2]), ";")[[1]]
  )
  g_ci_lwr[i] <- g_ci[1]
  g_ci_upr[i] <- g_ci[2]
  i <- i + 1
}

png(filename = file.path(basedir, "analysis/psilodep/paperfigs/SI_Fig_02.png"), res = 315, width = 2500, height = 1500)
# plot the results (base R with shaded CI ribbon)
y_vals <- c(g_ci_lwr, g_ci_upr, g_sweep)
y_finite <- y_vals[is.finite(y_vals)]
y_range <- suppressWarnings(range(y_finite))
if (!all(is.finite(y_range))) y_range <- c(-1, 1)

{
  plot(rho_seq, g_sweep,
    type = "n",
    xlab = "rho", ylab = "Hedges' g",
    xlim = range(rho_seq, na.rm = TRUE),
    ylim = y_range
  )

  mask_ci <- is.finite(g_ci_lwr) & is.finite(g_ci_upr) & is.finite(rho_seq)
  if (sum(mask_ci) >= 2) {
    polygon(c(rho_seq[mask_ci], rev(rho_seq[mask_ci])),
      c(g_ci_lwr[mask_ci], rev(g_ci_upr[mask_ci])),
      col = grDevices::adjustcolor("red", alpha.f = 0.2),
      border = NA
    )
  }

  lines(rho_seq, g_sweep, col = "blue", lwd = 2)
  lines(rho_seq, g_ci_lwr, col = "red", lty = 2)
  lines(rho_seq, g_ci_upr, col = "red", lty = 2)
}
dev.off()

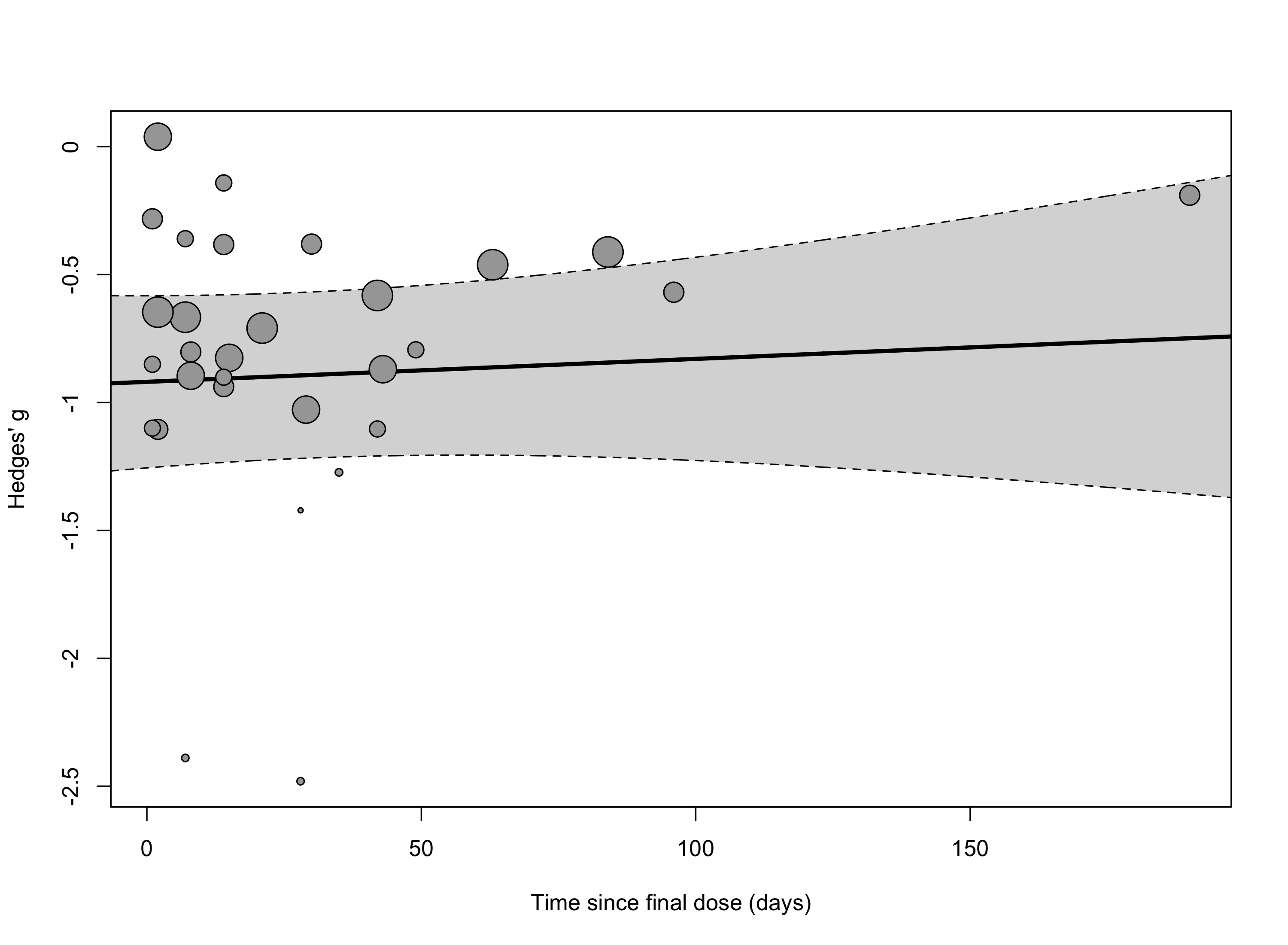
Meta-Regression

We perform meta-regression to examine the relationship between time since final dose and treatment effect.

reg <- metaRegression(time_results$model.threelevel.che, ~time_days)
reg

## 
## Multivariate Meta-Analysis Model (k = 37; method: REML)
## 
## Variance Components:
## 
##             estim    sqrt  nlvls  fixed       factor 
## sigma^2.1  0.0767  0.2770     12     no        study 
## sigma^2.2  0.0451  0.2123     37     no  study/es.id 
## 
## Test for Residual Heterogeneity:
## QE(df = 35) = 90.3819, p-val < .0001
## 
## Test of Moderators (coefficient 2):
## F(df1 = 1, df2 = 35) = 1.9272, p-val = 0.1738
## 
## Model Results:
## 
##            estimate      se     tval  df    pval    ci.lb    ci.ub      
## intrcpt     -0.8796  0.1307  -6.7275  35  <.0001  -1.1450  -0.6142  *** 
## time_days    0.0019  0.0013   1.3882  35  0.1738  -0.0009   0.0046      
## 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

png(filename = file.path(basedir, "analysis/psilodep/paperfigs/SI_Fig_03.png"), res = 315, width = 3000, height = 2200)
regplot(reg, mod = "time_days", xlab = "Time since final dose (days)", ylab = "Hedges' g")
dev.off()

Adding time since final dose as a continuous predictor to our model reveals a large and significant effect-size favoring psilocybin immediately following dosing that was stable over time.

Subgroup and Sensitivity Analyses

We conduct comprehensive subgroup and sensitivity analyses to examine the robustness of our findings and explore potential moderators of treatment effects.

These analyses include:

Subgroup Analyses:

  • MDD as primary diagnosis

  • Study design (parallel vs. crossover)

  • Exclusion of open-label studies

  • Exclusion of high risk-of-bias studies

Sensitivity Analyses:

  • In the multi-arm study (Goodwin 2022) replace high-dose intervention (25 mg) with medium-dose intervention (10 mg)

  • Expanded inclusion criteria

  • Clinician-rated vs. self-report outcomes

  • Exclusion of outlier studies

  • Fixed-effects model

# Build a dataframe for each subgroup and sensitivity analysis

data_dep <- data_main %>%
  filterPoolingData(
    diagnosis == "mdd" | diagnosis == "trd"
  )

data_excol <- data_main %>%
  filterPoolingData(
    !Detect(blinding, "open-label"),
  )

data_rob <- data_main %>%
  filterPoolingData(
    !Detect(rob, "High"),
  )

data_parallel <- data_main %>%
  filterPoolingData(
    design == "parallel"
  )

data_crossover <- data_main %>%
  filterPoolingData(
    design == "crossover"
  )

data_expanded <- data %>%
  filterPoolingData(
    primary_instrument == "1",
    primary_timepoint == "1",
    outcome_type == "msd" | outcome_type == "imsd",
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm1)) & Detect(multi_arm1, "10 mg")),
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm2)) & Detect(multi_arm2, "10 mg")),
    !(Detect(study, "Krempien 2023") & (!is.na(multi_arm1)) & Detect(multi_arm1, "12 mg")),
    !(Detect(study, "Krempien 2023") & (!is.na(multi_arm2)) & Detect(multi_arm2, "12 mg"))
  )

data_outliers <- data_main %>%
  filterPoolingData(
    !Detect(study, "Davis 2021")
  )

data_fixed <- data_main

data_g10 <- data %>%
  filterPoolingData(
    primary_instrument == "1",
    primary_timepoint == "1",
    is.na(post_crossover) | !Detect(post_crossover, "1"),
    outcome_type == "msd" | outcome_type == "imsd",
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm1)) & Detect(multi_arm1, "25 mg")),
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm2)) & Detect(multi_arm2, "25 mg")),
    !Detect(study, "Krempien 2023"),
    !Detect(study, "Carhart-Harris 2021")
  )

data_clinician <- data %>%
  filterPoolingData(
    primary_timepoint == "1",
    is.na(post_crossover) | !Detect(post_crossover, "1"),
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm1)) & Detect(multi_arm1, "10 mg")),
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm2)) & Detect(multi_arm2, "10 mg")),
    !Detect(study, "Krempien 2023"),
    !Detect(study, "Carhart-Harris 2021"),
    rating == "clinician",
    Detect(instrument_symptom, "depression"),
    outcome_type != "response",
    outcome_type != "remission",
    outcome_type != "change"
  ) %>%
  filterPriorityRule(instrument = c("madrs", "grid-ham-d"))

data_selfreport <- data %>%
  filterPoolingData(
    primary_timepoint == "1",
    is.na(post_crossover) | !Detect(post_crossover, "1"),
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm1)) & Detect(multi_arm1, "10 mg")),
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm2)) & Detect(multi_arm2, "10 mg")),
    !Detect(study, "Krempien 2023"),
    !Detect(study, "Carhart-Harris 2021"),
    rating == "self-report",
    Detect(instrument_symptom, "depression"),
    outcome_type != "response",
    outcome_type != "remission",
    outcome_type != "change" & outcome_type != "unknown"
  ) %>%
  filterPriorityRule(instrument = c("bdi-ii", "bid-1a", "bdi", "qids-sr", "hads-d", "smdds", "hads"))

Now we can use metapsyTools for quickly looking at subgroup and sensitivity results.

# Run the main "overall" model for comparison

main <- runMetaAnalysis(data_main,

  # Specify statistical parameters
  which.run = "overall", # inverse variance random effects
  es.measure = "g", # Hedges' g
  method.tau = "REML",
  method.tau.ci = "Q-Profile",
  hakn = TRUE, # Knapp-Hartung adjustment

  # Specify variables
  study.var = "study",
  arm.var.1 = "condition_arm1",
  arm.var.2 = "condition_arm2",
  measure.var = "instrument",
  w1.var = "n_arm1",
  w2.var = "n_arm2",
  time.var = "time_weeks",
  round.digits = 2
)

# Use metapsyTools' replacement and rerun functions for quickly changing parameters

dep <- main # copy the main model
data(dep) <- data_dep # replace the dataframe in the new model
dep <- rerun(dep) # re-run the model
dep

## Model results ------------------------------------------------ 
## Model       k     g g.ci          p        i2 i2.ci          prediction.ci   nnt
## .93 [-1.87; 0.01] 0.051  69.5 [21.89; 88.08] [-3; 1.14]     2.99

excol <- main
data(excol) <- data_excol
excol <- rerun(excol)
excol

## Model results ------------------------------------------------ 
## Model       k     g g.ci          p         i2 i2.ci      prediction.ci    nnt
## .81 [-1.03; -0.6] <0.001   2.9 [0; 65.82] [-1.03; -0.59]  3.46

rob <- main
data(rob) <- data_rob
rob <- rerun(rob)
rob

## Model results ------------------------------------------------ 
## Model       k     g g.ci           p         i2 i2.ci      prediction.ci    nnt
## .97 [-1.38; -0.57] <0.001  51.2 [0; 77.15] [-1.74; -0.21]  2.83

parallel <- main
data(parallel) <- data_parallel
parallel <- rerun(parallel)
parallel

## Model results ------------------------------------------------ 
## Model       k     g g.ci           p         i2 i2.ci      prediction.ci    nnt
## 0.8 [-1.11; -0.49] <0.001  35.5 [0; 72.79] [-1.06; -0.54]  3.52

crossover <- main
data(crossover) <- data_crossover
crossover <- rerun(crossover)
crossover

## Model results ------------------------------------------------ 
## Model       k     g g.ci           p        i2 i2.ci          prediction.ci   nnt
## .04 [-2.06; -0.03] 0.046  71.2 [26.88; 88.61] [-3.44; 1.35]  2.63

expanded <- main
data(expanded) <- data_expanded
expanded <- rerun(expanded)
expanded

## Model results ------------------------------------------------ 
## Model       k     g g.ci           p         i2 i2.ci          prediction.ci    nnt
## .88 [-1.21; -0.56] <0.001  54.8 [19.16; 74.75] [-1.72; -0.04]  3.16

outliers <- main
data(outliers) <- data_outliers
outliers<- rerun(outliers)
outliers

## Model results ------------------------------------------------ 
## Model       k     g g.ci           p         i2 i2.ci      prediction.ci    nnt
## .81 [-1.07; -0.55] <0.001  32.7 [0; 66.92] [-1.16; -0.46]  3.48

fixed <- main
method.tau(fixed) <- "FE" # for this sensitivity analysis, we keep data the same but change parameters
hakn(fixed) <- FALSE
fixed <- rerun(fixed)
fixed

## Model results ------------------------------------------------ 
## Model       k     g g.ci           p         i2 i2.ci          prediction.ci    nnt
## .84 [-1.02; -0.67] <0.001  53.9 [11.39; 75.98] [-1.73; -0.08]  3.32

g10 <- main
data(g10) <- data_g10
g10 <- rerun(g10)
g10

## Model results ------------------------------------------------ 
## Model       k     g g.ci           p         i2 i2.ci          prediction.ci   nnt
## .87 [-1.27; -0.47] <0.001  69.2 [44.08; 83.04] [-1.98; 0.25]  3.23

clinician <- main
data(clinician) <- data_clinician
clinician <- rerun(clinician)
clinician

## Model results ------------------------------------------------ 
## Model       k     g g.ci          p        i2 i2.ci          prediction.ci   nnt
## .02 [-1.6; -0.44] 0.005  64.5 [19.95; 84.25] [-2.28; 0.24]  2.71

selfreport <- main
data(selfreport) <- data_selfreport
selfreport <- rerun(selfreport)
selfreport

## Model results ------------------------------------------------ 
## Model       k     g g.ci           p        i2 i2.ci         prediction.ci   nnt
##  -1 [-1.68; -0.31] 0.010    73 [47.19; 86.2] [-2.76; 0.76]  2.76

We summarize these subgroup and sensitivity analyses in Figure 3 below. Our series of subgroup and sensitivity analyses produced results largely in line with our main model results. Hedges’ g values did not differ greatly from the main model, and 10/11 of the subgroup and sensitivity analyses produced significant results. Heterogeneity changes substantially when excluding open-label studies, excluding crossover studies, analyzing crossover studies on their own, and looking exclusively at self-report outcomes.

Bayesian implementation

As a final sensitivity analysis, we implement our main model using a bayesian framework. We do this using the bayesmeta package using “weakly informative prior distributions”.

Parameters: - A normal prior distribution with a 95% probability that the pooled estimate falls between -2 and 2. - A half-normal prior distribution for tau, with an s.d. of 0.5

bayes <- bayesmeta(
  data_main$.g,
  data_main$.g_se,
  mu.prior = c("mean"=0, "sd"=1), # asserts a 95% prior b/n -2 and 2
  tau.prior = function(t) dhalfnormal(t, scale = 0.5)
  )
bayes

##  'bayesmeta' object.
## 
## 12 estimates:
## 01, 02, 03, 04, 05, 06, 07, 08, 09, 10, ...
## 
## tau prior (proper):
## function (t) 
## dhalfnormal(t, scale = 0.5)
## <bytecode: 0x322a97540>
## 
## mu prior (proper):
## normal(mean=0, sd=1)
## 
## ML and MAP estimates:
##                    tau         mu
## ML joint     0.2770728 -0.8910220
## ML marginal  0.3362330 -0.8749251
## MAP joint    0.2268222 -0.8693622
## MAP marginal 0.2898848 -0.8625754
## 
## marginal posterior summary:
##                 tau         mu
## mode      0.2898848 -0.8625754
## median    0.2990692 -0.8714675
## mean      0.3127251 -0.8763131
## sd        0.1835568  0.1426918
## 95% lower 0.0000000 -1.1694173
## 95% upper 0.6373571 -0.5981181
## 
## (quoted intervals are shortest credible intervals.)

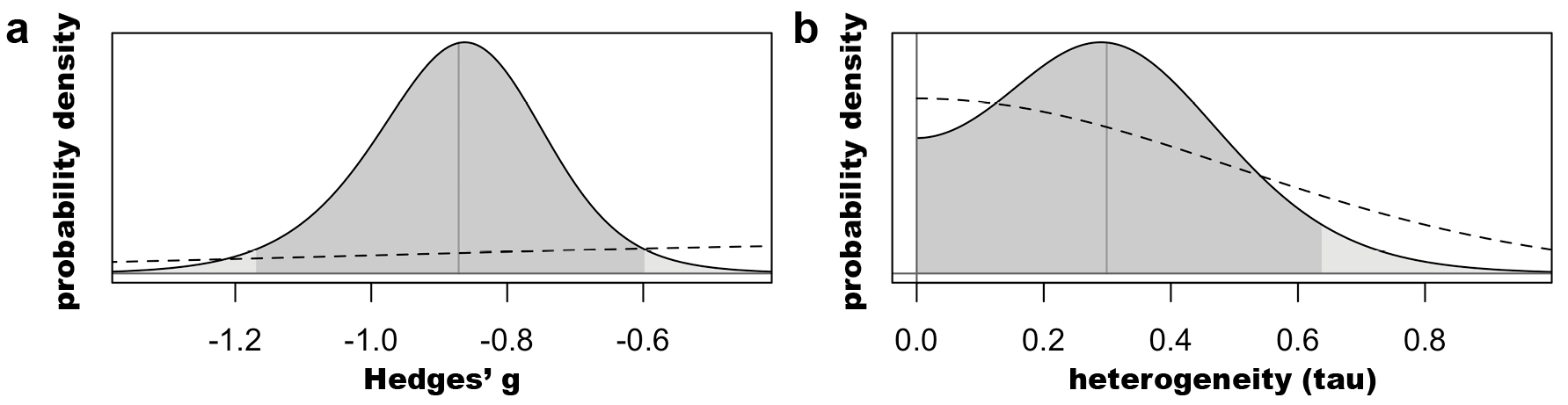
Above we can see the characteristics of the marginal posterior distributions of tau and mu (the pooled estimate). The model finds that the 95% interval of the true effect lies between -1.17 and -0.60.

We can visualize each posterior probability distribution (solid line), along with the priors (dashed) below:

Dichotomous Outcomes Analysis

In addition to continuous depression severity scores, we also analyze dichotomous outcomes including response and remission rates. These analyses provide complementary information about the clinical significance of psilocybin treatment.

Response Rate Analysis

We first analyze response rates, defined as the proportion of participants achieving a clinically meaningful reduction in depression symptoms.

# Get response data

data_response <- data %>%
  filterPoolingData(
    primary_instrument == "1",
    primary_timepoint == "1",
    outcome_type == "response",
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm1)) & Detect(multi_arm1, "10 mg")),
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm2)) & Detect(multi_arm2, "10 mg")),
    !Detect(study, "Krempien 2023")
  )
data_response <- data_response[order(data_response$year), ]

# Run meta-analysis

response_results <- runMetaAnalysis(data_response,
  which.run = "overall",
  es.measure = "RR", # risk ratio
  es.type = "raw",
  method.tau = "PM",
  method.tau.ci = "Q-Profile",
  method.random.ci = "HK",
  hakn = TRUE, # Knapp-Hartung adjustement

  # Specify variables
  study.var = "study",
  arm.var.1 = "condition_arm1",
  arm.var.2 = "condition_arm2",
  measure.var = "instrument",
  w1.var = "n_arm1",
  w2.var = "n_arm2",
  time.var = "time_weeks",
  round.digits = 2
)

# Create simple forest plot of response results

meta::forest(
  response_results$model.overall,
  sortvar = response_results$model.overall$data$year,
  xlab = "Log RR (95% CI)",
  leftlabs = c("Study", "Log RR"),
  layout = "JAMA"
)

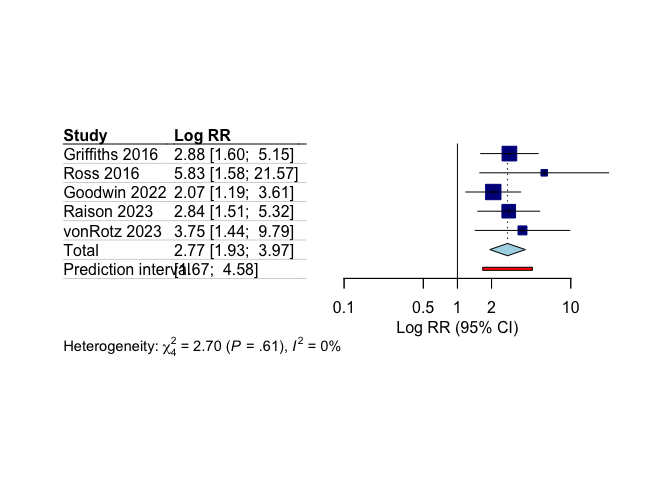
Our meta-analysis shows statistically significant greater treatment response with psilocybin compared to control conditions.

Remission Rate Analysis

We also analyze remission rates, defined as the proportion of participants achieving full remission of depressive symptoms.

# Get remission data

data_remission <- data %>%
  filterPoolingData(
    primary_instrument == "1",
    primary_timepoint == "1",
    outcome_type == "remission",
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm1)) & Detect(multi_arm1, "10 mg")),
    !(Detect(study, "Goodwin 2022") & (!is.na(multi_arm2)) & Detect(multi_arm2, "10 mg")),
    !Detect(study, "Krempien 2023")
  )
data_remission <- data_remission[order(data_remission$year), ]

# Run meta-analysis

remission_results <- runMetaAnalysis(data_remission,
  which.run = "overall",
  es.measure = "RR", # risk ratio
  es.type = "raw",
  method.tau = "PM",
  method.tau.ci = "Q-Profile",
  method.random.ci = "HK",
  hakn = TRUE, # Knapp-Hartung adjustement

  # Specify variables
  study.var = "study",
  arm.var.1 = "condition_arm1",
  arm.var.2 = "condition_arm2",
  measure.var = "instrument",
  w1.var = "n_arm1",
  w2.var = "n_arm2",
  time.var = "time_weeks",
  round.digits = 2
)

# Create simple forest plot of remission results

meta::forest(
  remission_results$model.overall,
  sortvar = remission_results$model.overall$data$year,
  xlab = "Log RR (95% CI)",
  leftlabs = c("Study", "Log RR"),
  layout = "JAMA"
)

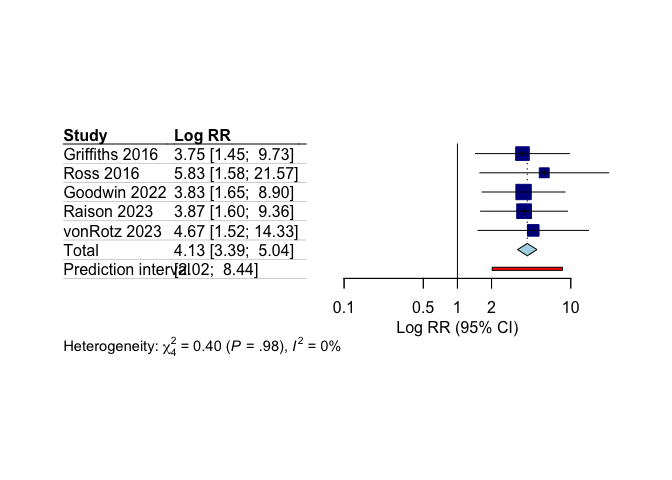
Our meta-analysis shows statistically significant higher remission rates with psilocybin compared to control conditions.

As a sensitivity analysis, we also run a fixed-effects meta-analysis on the response and remission results.

# Fixed response
method.tau(response_results) <- "FE"
hakn(response_results) <- FALSE
rerun(response_results)

## Model results ------------------------------------------------ 
## Model       k    rr rr.ci        p         i2 i2.ci     prediction.ci   nnt
## 2.8 [2.05; 3.83] <0.001     0 [0; 79.2] [1.67; 4.58]   2.81

# Fixed remission
method.tau(remission_results) <- "FE"
hakn(remission_results) <- FALSE
rerun(remission_results)

## Model results ------------------------------------------------ 
## Model       k    rr rr.ci        p         i2 i2.ci      prediction.ci   nnt
## .05 [2.67; 6.15] <0.001     0 [0; 74.62] [2.23; 7.31]   2.98

Our fixed effects models yielded results that were in line with the main model, showing statistically significant higher response and remission rates with psilocybin compared to control conditions.

Summary and Conclusions

This comprehensive meta-analysis provides promising evidence regarding the efficacy of psilocybin for treating depression, but should be interpreted with caution.

The analysis includes:

  1. Primary analysis of continuous depression severity outcomes using standardized mean differences
  2. Time course analysis examining how treatment effects evolve over time
  3. Publication bias assessment using multiple methods
  4. Extensive subgroup and sensitivity analyses to examine robustness and moderators
  5. Dichotomous outcomes analysis of response and remission rates

The results demonstrate consistent evidence for the efficacy of psilocybin in reducing depression severity, with effects persisting over time and showing robustness across various sensitivity analyses. However, given the small number of studies eligible to include in our meta-analysis and limitations such as the potential for functional unblinding and expectancy effects, results should be interpreted with caution.